Jika Sahabat ingin mengolah data kuantitatif dan ingin mengetahui hubungan antara dua variabel, bisa menggunakan uji regresi linier sederhana atau simple linear regression. Teknik regresi linier ini sudah banyak membantu peneliti dalam melihat apakah kedua variabel saling mempengaruhi atau tidak.
Idealnya, pendekatan ini membantu memahami seberapa kuat korelasi antara kedua variabel dan bagaimana perubahan pada satu variabel dapat mempengaruhi variabel lain. Artinya, regresi linier tipe sederhana ini merupakan alat untuk memprediksi nilai satu variabel berdasarkan nilai variabel lainnya.
Mengenal Regresi Linier Sederhana
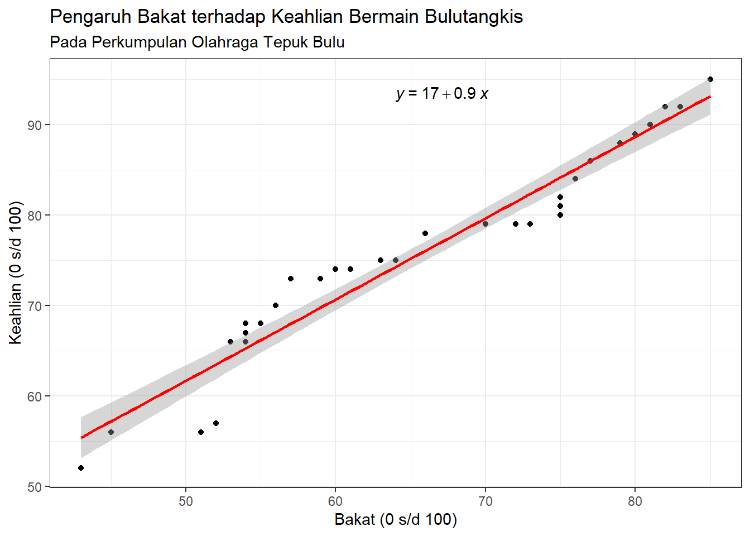
Regresi linier sederhana adalah teknik statistik yang digunakan untuk memodelkan dan menganalisis hubungan antara dua variabel kuantitatif. Dalam teknik ini, satu variabel dianggap sebagai variabel dependen (Y), dan variabel lainnya dianggap sebagai variabel independen (X).
Rumus atau persamaan regresi linear sederhana adalah sebagai berikut:
Y = β0 +β1X + ϵ
Keterangan:
- Y adalah variabel dependen (yang ingin kita prediksi).
- X adalah variabel independen (penyebab perubahan Y).
- β0 adalah konstanta atau intersep (nilai Y saat X = 0).
- β1 adalah koefisien regresi (menunjukkan perubahan dalam Y untuk setiap perubahan satu unit dalam X).
- ε adalah kesalahan acak (menunjukkan variasi Y yang tidak dijelaskan oleh model).
Uji Hipotesis
Uji hipotesis regresi linier sederhana digunakan untuk menguji apakah ada hubungan yang signifikan antara variabel independen (X) dan variabel dependen (Y). Berikut langkah-langkah dan komponen dasar dari uji hipotesis ini:
- Hipotesis Nol (H0), artinya tidak ada hubungan antara variabel X dan variabel Y.
- Hipotesis Alternatif (Ha), artinya koefisien regresi tidak sama dengan nol, yang berarti ada hubungan antara X dan Y.
- Menghitung statistik uji dengan formula uji t, yaitu (b adalah koefisien regresi yang diestimasi dari sampel data, β adalah nilai hipotesis nol, dan SE(b) adalah kesalahan standar dari koefisien regresi.
- Bandingkan dengan nilai kritis, biasanya tingkat signifikansinya adalah 0,05. Jika nilai t yang dihitung lebih besar dari nilai kritis, maka tolak H0.
Jika H0 ditolak, Sahabat bisa menyimpulkan bahwa ada hubungan yang signifikan antara X dan Y. Jika H0 tidak ditolak, maka tidak ada bukti yang cukup untuk mengatakan ada hubungan yang signifikan antara X dan Y.
Baca Juga: Pengertian Uji Validitas dan Reliabilitas + Rumusnya (Terlengkap)
Asumsi Regresi Linier Sederhana
Uji regresi linear sederhana adalah pendekatan yang cukup unik karena melibatkan asumsi-asumsi tertentu. Dalam melakukan analisis simple linear regression terdapat beberapa asumsi yang harus dipenuhi agar hasil analisis dapat diinterpretasikan dengan benar dan valid. Berikut adalah asumsi-asumsinya:
1. Linearitas Hubungan
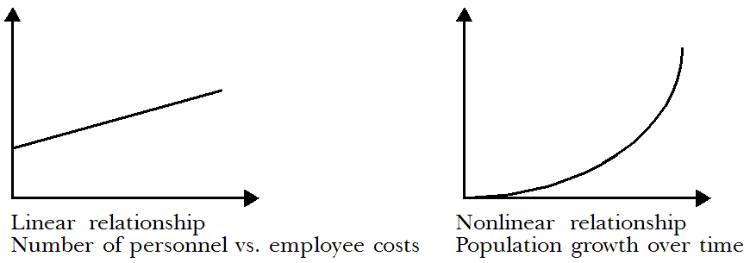
Hubungan antara variabel independen (X) dan variabel dependen (Y) harus linear. Hal ini dapat dicek dengan melihat scatterplot antara X dan Y. Asumsi ini berkaitan dengan bagaimana bentuk hubungan antara kedua variabel tersebut. Idealnya, relasi antara keduanya seharusnya mengikuti pola linear.
Dengan kata lain, saat variabel X berubah, perubahan pada variabel Y harus dapat dijelaskan melalui hubungan linier. Salah satu metode paling sederhana dan visual untuk memeriksa asumsi ini adalah dengan membuat scatterplot, yakni grafik yang menampilkan titik-titik data dari kedua variabel tersebut.
Dengan memvisualisasikan data melalui scatterplot, Sahabat bisa dengan mudah melihat dan memastikan apakah pola hubungan antara X dan Y linear atau tidak. Jika titik-titik data cenderung mengikuti garis lurus atau mendekati garis lurus, maka mengindikasikan bahwa hubungan X dan Y memang bersifat linier.
2. Independensi Residual
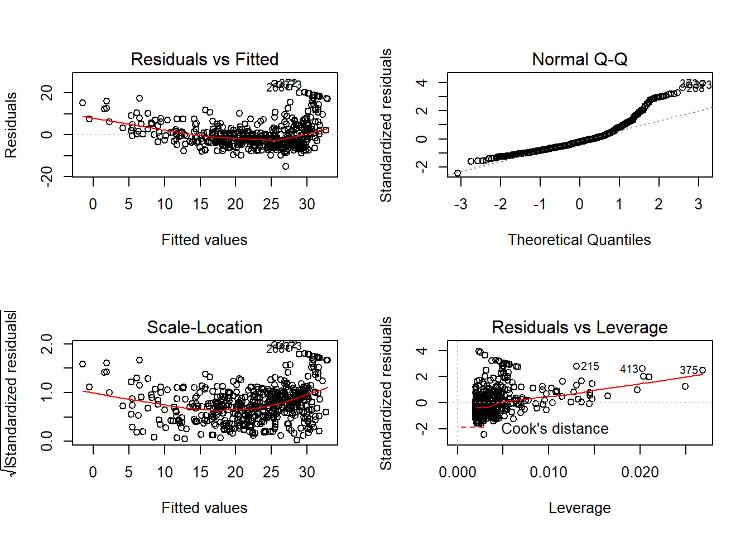
Residual merupakan perbedaan antara apa yang diamati dengan apa yang diperkirakan oleh model. Pada dasarnya, mereka merepresentasikan bagian dari data yang belum dijelaskan oleh model. Sangat penting bahwa residual ini bebas dari ketergantungan satu sama lain.
Apabila berbicara dalam lingkup analisis waktu-seri, ini mengindikasikan adanya ketidakhadiran autokorelasi. Autokorelasi terjadi ketika sebuah nilai dalam suatu urutan terkait dengan nilai lain pada interval waktu tertentu.
Dengan kata lain, nilai saat ini memiliki hubungan dengan nilai sebelumnya. Dalam analisis regresi, idealnya kita menginginkan residual yang bersifat acak, sehingga tidak ada pola tertentu yang dapat dikenali dalam residu.
Jika ada autokorelasi, ini bisa menjadi tanda bahwa Sahabat belum memasukkan beberapa informasi penting dari data. Dengan memastikan residual independen dan bebas dari autokorelasi, maka Sahabat dapat lebih percaya diri bahwa data memberikan representasi akurat dari hubungan dua variabel.
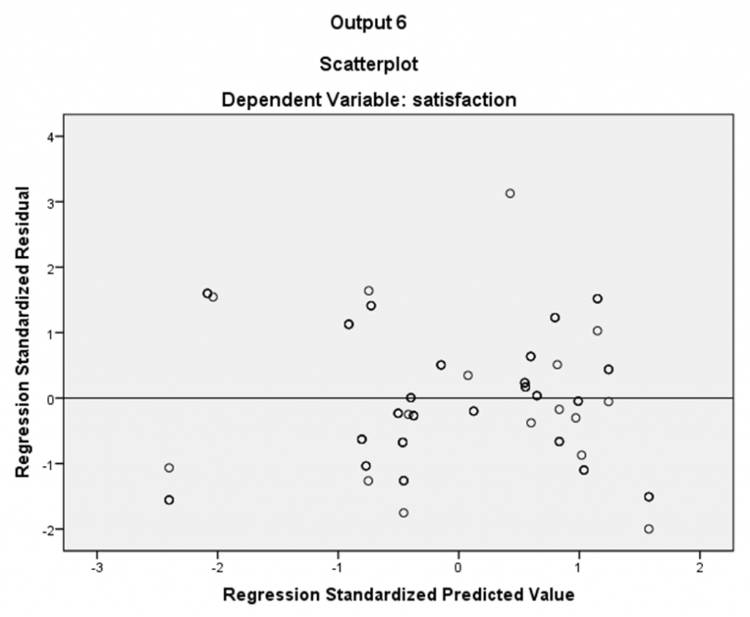
3. Homoskedastisitas
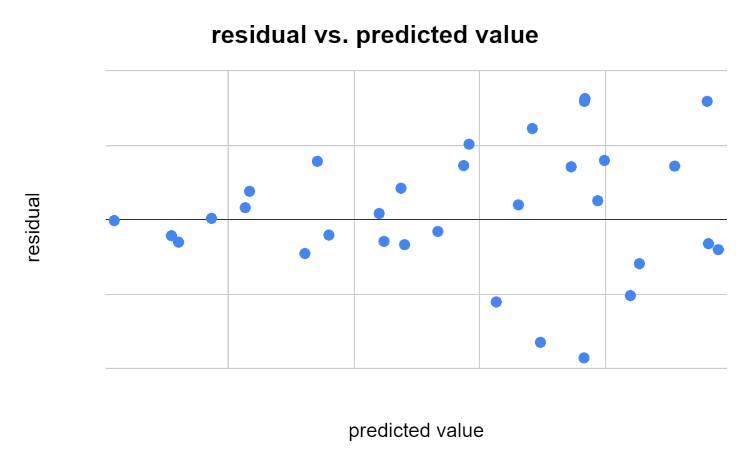
Variansi dari residual harus konstan di seluruh level variabel independen. Sebagai ilustrasi, jika X naik, residual tidak seharusnya menjadi lebih bervariasi atau lebih stabil. Sebaliknya, residual harus memiliki kekonsistenan yang sama, tidak peduli apakah X sedang rendah atau tinggi.
4. Tidak Ada Multikolinearitas

Meskipun asumsi ini lebih relevan untuk regresi linier berganda (di mana ada lebih dari satu variabel independen), dalam konteks analisis regresi linier sederhana, ide dasarnya adalah variabel independen tidak boleh tergantung pada variabel lain.
5. Tidak Ada Endogenitas
Variabel dependen tidak boleh dipengaruhi oleh kesalahan (error term). Dengan kata lain, kesalahan atau gangguan tidak boleh berkorelasi dengan variabel independen. Singkatnya, integritas dan keakuratan dari variabel dependen harus terjaga, memastikan bahwa tidak ada distorsi.
Setiap bentuk ketidaksesuaian atau gangguan yang mungkin mempengaruhi hasil harus dikelola agar tidak menciptakan bias dalam interpretasi hubungan antara variabel independen dan dependen. Dalam konteks pemodelan statistik, prinsip ini sangat penting untuk memastikan bahwa hasilnya valid.
Pemenuhan asumsi-asumsi diatas penting untuk memastikan bahwa model regresi linier memberikan estimator yang BLUE (Best Linear Unbiased Estimator). Jika beberapa asumsi tersebut tidak terpenuhi, mungkin diperlukan teknik analisis lanjutan atau transformasi data untuk memenuhi asumsinya.
Baca Juga: Cara Menghitung Daya UPS Untuk Server, Komputer dan Lainnya
Kegunaan Regresi Linier Sederhana
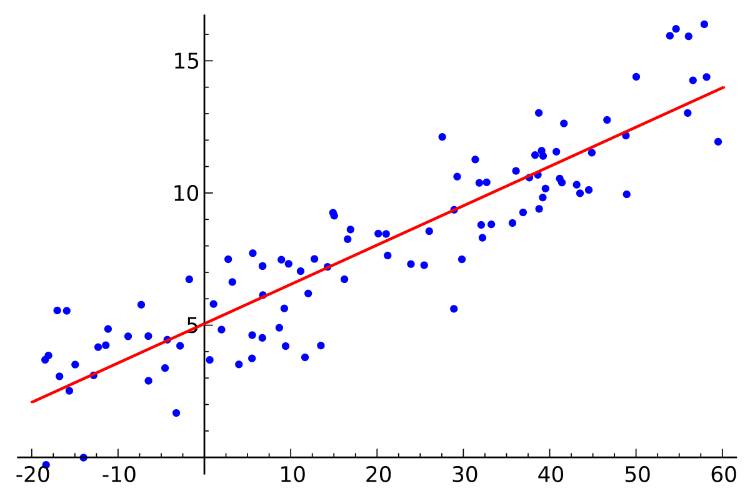
Sebenarnya, regresi linear sederhana untuk apa? Sebagai salah satu teknik dalam statistik atau olah data, regresi linier sederhana adalah jenis regresi yang digunakan ketika:
- Ada satu variabel independen dan satu variabel dependen, yaitu jika Sahabat tertarik untuk memeriksa bagaimana satu variabel (variabel independen atau prediktor) mempengaruhi variabel lain (variabel dependen atau respons).
- Hubungan antara variabel dianggap linier atau perubahan pada variabel independen diharapkan menyebabkan perubahan proporsional pada variabel dependen.
- Ingin memprediksi atau menjelaskan variasi sehingga dapat mengestimasi hubungan antara dua variabel dan kemudian menggunakan model tersebut untuk membuat prediksi.
- Dalam situasi di mana hanya ada satu prediktor dan tidak ada kebutuhan untuk model yang lebih kompleks, teknik ini dapat digunakan sebagai alat yang tepat.
- Biasanya digunakan untuk data yang bersifat kuantitatif, meskipun dapat digunakan untuk variabel kategorikal yang dikodekan dengan tepat.
- Asumsi-asumsi dasar terpenuhi, termasuk normalitas residu, homoskedastisitas (varians konstan dari residu), dan tidak adanya autokorelasi.
Jika ada lebih dari satu variabel independen yang dianggap memiliki pengaruh terhadap variabel dependen, atau jika hubungan antara variabel-variabel tersebut dianggap tidak linier, maka jenis regresi lain seperti regresi linier berganda atau regresi non-linier mungkin lebih sesuai.
Kesimpulan
Regresi linier sederhana adalah suatu teknik statistik yang digunakan untuk memodelkan dan menganalisis hubungan antara dua variabel. Teknik ini menghasilkan suatu garis lurus yang paling sesuai dengan data dengan tujuan untuk menggambarkan seberapa kuat hubungan antara kedua variabel.

