Rumus Diagram Venn Lengkap dengan Contoh + Pembahasan

Himpunan ternyata bisa diilustrasikan dalam sebuah diagram Venn yang bisa menggambarkan himpunan yang saling berhubungan. Himpunan menjadi elemen utama dalam diagram Venn. Sebelum membahas lebih lanjut tentang rumus diagram Venn, alangkah baiknya paham dengan himpunan.

Tanpa adanya himpunan, maka diagram Venn tidak dapat disusun. Adanya diagram Venn bisa mempermudah mengetahui hubungan antar himpunan. Diagram Venn biasanya hanya terdiri dari 2 himpunan saja, namun ada juga yang menggunakan 3 himpunan.

Table of Contents

Apa itu Diagram Venn?

Diagram Venn merupakan gambar yang dipakai untuk menunjukkan hubungan antara himpunan dalam suatu kelompok objek yang mempunyai kesamaan nilai.

Diagram Venn ini biasanya digunakan untuk menggambarkan himpunan yang saling lepas, berpotongan, dan lainnya. Biasanya digunakan untuk menyajikan data secara teknik dan saintifik dan bermanfaat di bidang matematika, statistik, hingga aplikasi komputer.

Bentuk Diagram Venn

Ada beberapa bentuk diagram Venn, diantaranya sebagai berikut.

1. Himpunan Bagian

Himpunan A bisa disebut sebagai bagian dari himpunan B jika seluruh anggota himpunan A adalah anggota himpunan B.

2. Himpunan Berpotongan (Irisan)

Diagram Venn ini menggambarkan himpunan yang saling berpotongan dikarenakan memiliki kesamaan. Himpunan A yang berpotongan dengan himpunan B bisa ditulis A ∩ B.

3. Himpunan Saling Lepas

Dikatakan himpunan saling lepas apabila himpunan A tidak sama dengan anggota himpunan B. penulisan himpunan saling lepas yaitu A//B.

4. Himpunan dengan Jumlah Sama

Diagram Venn ini menunjukkan bahwa apabila himpunan A dan B memiliki anggota himpunan yang sama, maka bisa disimpulkan bahwa setiap anggota A adalah anggota B. Misalnya A = {1,2,3} dan B= {3,2,1} adalah himpunan yang sama. Oleh karena itu bisa ditulis A = B.A

5. Himpunan yang Ekuivalen

Dikatakan ekuivalen apabila himpunan A dan B memiliki banyak anggota yang sama. Himpunan A yang ekuivalen dengan himpunan B bisa ditulis dengan n(A) = n(B).

Hubungan Antar Himpunan

Pada diagram Venn, ada empat hubungan antar-himpunan, yaitu irisan, gabungan, dan komplemen.

1. Irisan

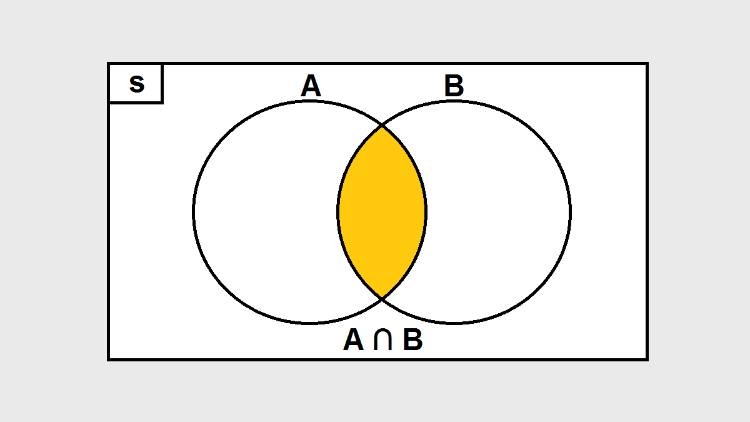
Irisan himpunan A dan B atau bisa ditulis dengan (A ∩ B) merupakan himpunan yang anggota-anggotanya terdapat di dalam himpunan A dan himpunan B.

Contohnya himpunan A = { 2,4,6,8,10,12} dan himpunan B = {2,3,4,5,6}. Kedua himpunan ini memiliki tiga anggota yang sama yaitu 2, 4, dan 6.

Karena kesamaan anggota himpunan inilah dapat disebut bahwa irisan himpunan A dan B (A ∩ B) = {2,4,6}.

2. Gabungan

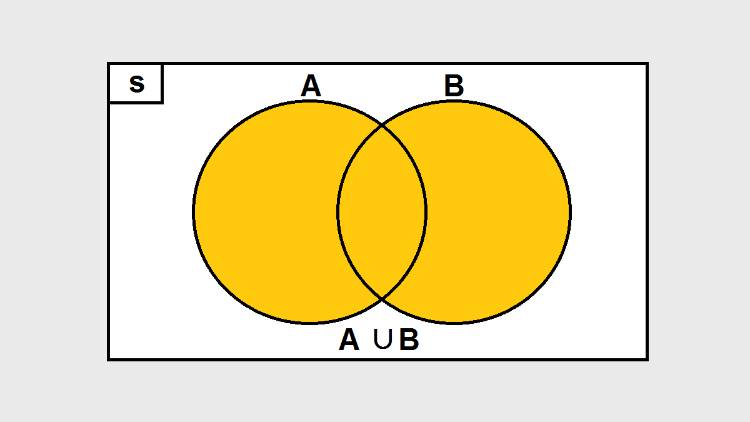
Gabungan himpunan A dan B atau bisa ditulis dengan (A ∪ B) merupakan himpunan yang anggotanya yaitu gabungan kedua himpunan A dan B.

contohnya himpunan A = {2,4,6,8,10,12,14} dan B= {1,2,3,4,5,6,7}. Apabila himpunan A dan B digabungkan, maka anggota himpunan barunya yaitu A ∪ B = {1,2,3,4,5,6,7,8,10,12,14}.

3. Komplemen

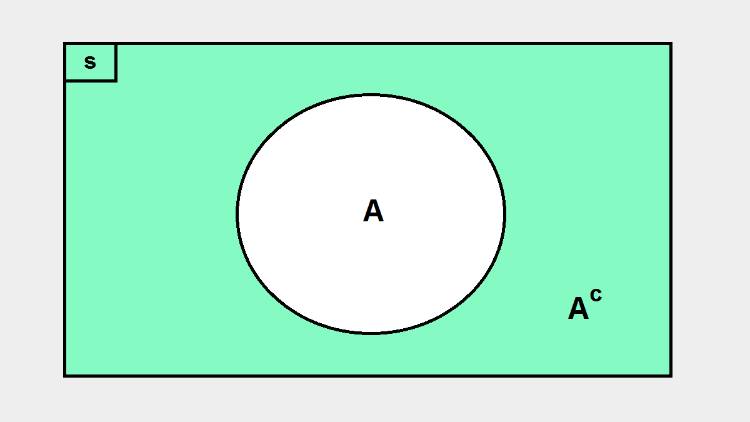
Komplemen himpunan atau bisa ditulis dengan (A^c) merupakan himpunan yang mana anggota-anggotanya adalah anggota himpunan semesta, tapi bukan anggota himpunan A.

Contohnya himpunan S = {1,2,3,4,5,6,7} dan A = {1,3,5,7}. Dapat diketahui bahwa seluruh anggota S yang bukan merupakan anggota himpunan A akan membentuk himpunan baru yaitu {2,4,6}. Komplemen dari himpunan A yaitu A^c = {2,4,6}.

Rumus Diagram Venn

Berikut rumus menentukan diagram Venn untuk dua dan tiga elemen:

n (A ∪ B) = n (A) + n (B) – n (A ∩ B)

n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)

Untuk lebih jelasnya, perhatikan gambar diagram Venn irisan dua himpunan di bawah ini!

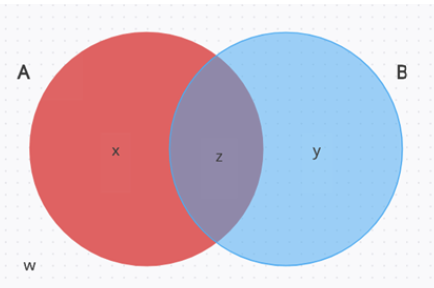
Dari gambar diagram Venn irisan dan gabungan tersebut dapat diketahui bahwa:

n (A) = x + z;

n (B) = y + z;

n (A ∩ B) = z;

n (A ∪ B) = x + y + z.

Jumlah total elemen = x + y + z + w

Keterangan:

x = jumlah elemen yang ada dalam himpunan A.

y = jumlah elemen yang ada dalam himpunan B.

z = jumlah elemen yang ada dalam himpunan A maupun B (A Ç B)

w = jumlah elemen yang tidak masuk dalam himpunan A atau B

Contoh Soal

Berikut contoh soal cerita beserta cara menghitung menggunakan rumus diagram Venn dan jawabannya.

Dalam sebuah survey yang dilakukan pada 400 mahasiswa di sebuah kampus, sebanyak 48% mahasiswa suka menonton bulutangkis, 54% mahasiswa suka menonton sepak bola, 60% mahasiswa suka menonton voli. Juga 29% mahasiswa suka menonton bulutangkis dan sepak bola, 27% mahasiswa suka menonton voli dan sepakbola, 25% mahasiswa suka bulutangkis dan voli, dan 4% mahasiswa tidak suka menonton olahraga ini.

Hitung

Berapa persentase mahasiswa yang suka menonton ketiga jenis olahraga tersebut?
Gambarkan diagram Venn dari soal tersebut!
Berapa jumlah mahasiswa yang hanya suka menonton satu dari ketiga jenis olahraga tersebut?
Berapa jumlah mahasiswa yang suka menonton setidaknya dua jenis olahraga tersebut?

Penyelesaian

Diketahui:

n (B) = persentase mahasiswa yang suka menonton bulutangkis = 48%

n (S) = persentase mahasiswa yang suka menonton sepak bola = 54%

n (V) = persentase mahasiswa yang suka menonton voli = 60%

n (B ∩ S) = 29%; n (V ∩ S) = 27%; n (B ∩ V) = 25%;

karena sebanyak 4% tidak suka menonton olahraga, maka n (B ∪ S ∪ V) = 96%.

Jawab:

untuk mengetahui persentase mahasiswa yang suka menonton ketiga jenis olahraga tersebut, maka gunakan rumus diagram Venn berikut ini:

n (B ∪ S ∪ V) = n (B) + n (S) + n (V) – n (B ∩ S) – n (V ∩ S) – n (B ∩ V) + n (B ∩ S ∩ V)

96% = 48% + 54% + 60% – 29% – 27% – 25% + n (B ∩ S ∩ V)

96% = 81 + n (B ∩ S ∩ V)

n (B ∩ S ∩ V) = 15%

Jadi, persentase mahasiswa yang suka menonton ketiga jenis olahraga tersebut yaitu 15%.

Gambar diagram Venn

Jumlah mahasiswa yang hanya suka menonton satu dari ketiga jenis olahraga tersebut yaitu:

(9% + 13% + 23%) x 400 = 180 mahasiswa.

Jumlah mahasiswa yang suka menonton minimal dua jenis olahraga tersebut yaitu:

(12% + 14% + 10% + 15%) x 400 = 204 mahasiswa.

Kesimpulan

Itulah penjelasan terkait rumus diagram Venn lengkap dengan pembahasan soal. Diagram Venn sangat berguna untuk menggambarkan hubungan antar himpunan. Himpunan menjadi elemen yang paling penting, karena tanpa adanya himpunan, diagram Venn tidak dapat dibuat.