Apa itu Probabilitas dalam Statistika? Ini Cara Menghitungnya

Probabilitas dan statistika adalah dua hal yang tidak dapat dipisahkan satu sama lain. Jika Sahabat sedang belajar statistika, maka istilah teori peluang atau kemungkinan terjadinya suatu peristiwa ini bisa saja ikut dipelajari juga.

Analisis probability ini memiliki banyak kegunaan jika bisa menerapkannya dalam kehidupan sehari-hari. Begitu pula dalam proses pembuatan keputusan penting. Tentunya, bukan hanya pada penelitian saja. Oleh karena itu, Sahabat harus memahaminya lebih lanjut dengan penjelasan berikut!

Table of Contents

Apa itu Probabilitas?

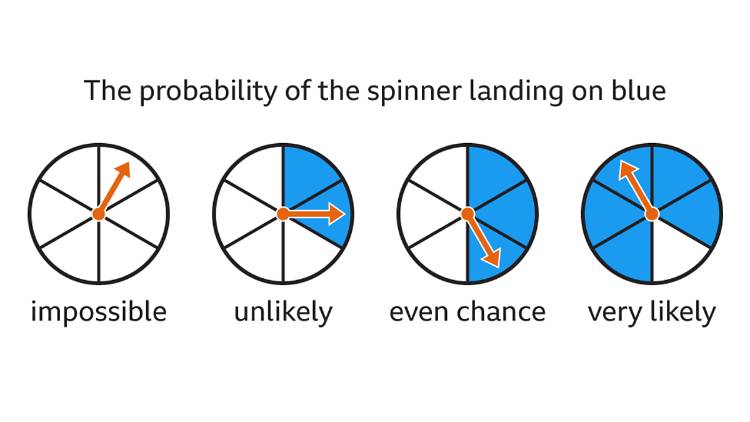
Teori probabilitas adalah ukuran yang menunjukkan seberapa besar kemungkinan suatu kejadian akan terjadi. Nilai peluang berkisar antara 0 dan 1; di mana nilai 0 menunjukkan bahwa kejadian tersebut tidak mungkin terjadi, dan nilai 1 menunjukkan bahwa kejadian tersebut pasti akan terjadi.

Istilah ini sering digunakan dalam statistik, matematika, dan ilmu pengetahuan alam untuk memprediksi, menganalisis, atau menjelaskan fenomena tertentu berdasarkan data yang ada. Dalam konteks sehari-hari, juga sering dihubungkan dengan risiko, ketidakpastian, atau peluang suatu kejadian terjadi.

Cara Menghitung Probabilitas

Menghitung teori kemungkinan ini pada dasarnya adalah menentukan peluang terjadinya suatu kejadian. Peluang terjadinya suatu kejadian selalu bernilai antara 0 dan 1, di mana 0 berarti kejadian tersebut tidak mungkin terjadi dan 1 berarti kejadian tersebut pasti terjadi.

1. Sederhana

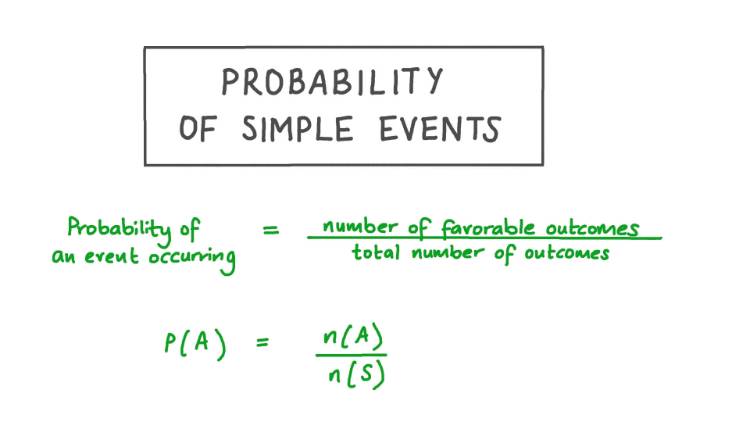
Probabilitas sederhana merujuk pada peluang dasar dari terjadinya suatu kejadian tanpa memperhatikan kondisi atau kejadian lain yang mungkin berpengaruh. Dalam konteks sehari-hari, Sahabat mungkin bertanya-tanya tentang peluang hujan besok, peluang tim kesayangan menang, dan lain sebagainya.

Rumus:

Contoh soal, jika Sahabat melempar dadu standar dengan 6 sisi, kemungkinan mendapatkan angka 3 adalah P(3) = . Hasil tersebut diperoleh karena hanya ada satu cara untuk mendapatkan angka 3 dari 6 kemungkinan hasil.

2. Gabungan

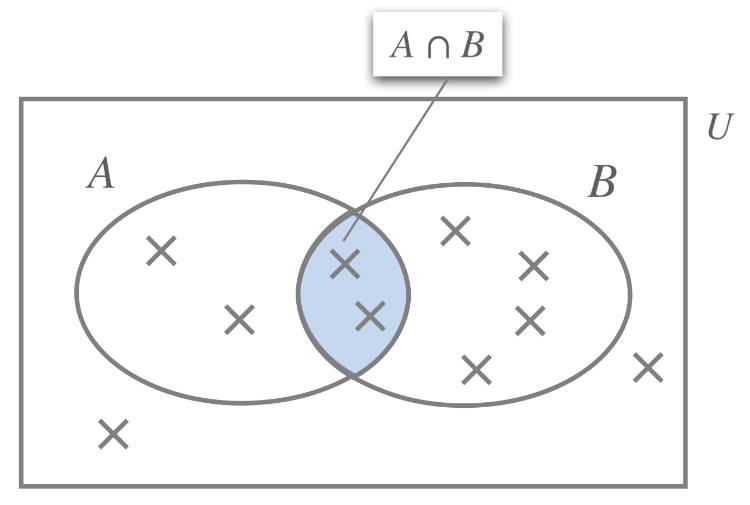
Probabilitas atau peluang gabungan merujuk pada peluang terjadinya salah satu dari dua kejadian atau keduanya secara bersamaan. Jika dua kejadian saling eksklusif, berarti kedua kejadian tersebut tidak bisa terjadi bersama-sama.

Sebagai contoh, saat melempar koin, Sahabat tidak bisa mendapatkan hasil kepala dan angka secara bersamaan. Sebaliknya, untuk kejadian yang tidak saling eksklusif, keduanya bisa terjadi bersamaan. Misalnya, seseorang bisa saja memenangkan dua jenis lotere berbeda pada hari yang sama.

Jika A dan B adalah dua kejadian yang saling eksklusif (tidak dapat terjadi bersama-sama), maka kemungkinan salah satu dari mereka terjadi bisa digambarkan dengan rumus probabilitas kombinasi P(A atau B) = P(A) + P(B).

3. Bersyarat

Probabilitas bersyarat mengacu pada peluang suatu kejadian terjadi dengan mempertimbangkan informasi tambahan dari kejadian lain yang sudah diketahui terjadi. Dengan kata lain, memberikan informasi tentang peluang suatu kejadian, berdasarkan pengetahuan bahwa kejadian lain sudah terjadi.

Sebagai contoh, bayangkan ingin mengetahui peluang seseorang memiliki rambut merah, tetapi sudah tahu bahwa orang tersebut memiliki mata biru. Peluang bersyarat akan memberikan peluang seseorang memiliki rambut merah dengan mempertimbangkan informasi bahwa orang tersebut memiliki mata biru.

Peluang suatu kejadian A terjadi, dengan syarat kejadian B sudah terjadi, dinotasikan dengan P(A|B) dan dapat dihitung menggunakan rumus:

Kegunaan Probabilitas

Mempelajari distribusi probabilitas memberikan berbagai manfaat, baik itu dari segi pengolahan data maupun dalam kehidupan sehari-hari. Berikut penjelasan mengenai kegunaannya:

1. Pengambilan Keputusan

Teori peluang ini membantu dalam pengambilan keputusan yang lebih tepat dan rasional. Dalam bisnis, pemerintahan, atau kehidupan sehari-hari, keputusan seringkali harus diambil dengan mempertimbangkan risiko dan ketidakpastian.

Dengan memahami distribusi peluang ini, seseorang dapat memperkirakan peluang hasil tertentu dan membuat keputusan yang lebih berdasar. Dengan begitu, suatu keputusan dapat dipilih setelah melalui serangkaian proses analisis tersebut.

2. Penelitian dan Data Analisis

Dalam dunia penelitian, probabilitas menjadi salah satu kunci dalam memastikan validitas dan reliabilitas dari suatu studi. Setiap peneliti berkeinginan untuk memahami sejauh mana temuan mereka bisa diandalkan dan apakah hasil tersebut bukan sekedar kebetulan.

Ketika menguji hipotesis, peneliti biasanya menentukan tingkat signifikansi atau batas peluang di mana peneliti bersedia untuk mengambil risiko dalam membuat kesalahan. Misalnya, jika peneliti menggunakan tingkat signifikansi 5%, berarti bersedia menerima risiko 5% bahwa kesimpulan yang dibuat mungkin salah.

Selain itu, konsep peluang ini juga membantu dalam interpretasi data. Dalam survei atau eksperimen, jarang sekali ada hasil yang 100% pasti. Dengan memahami pendekatan ini, peneliti dapat menilai kemungkinan suatu hasil terjadi berdasarkan data yang dikumpulkan.

3. Mengukur Derajat Ketidakpastian

Probabilitas adalah konsep matematika yang memberikan alat untuk mengukur derajat ketidakpastian. Dalam kehidupan sehari-hari, seringkali dihadapkan dengan situasi di mana hasil dari suatu peristiwa tidak pasti.

Misalnya, kita melempar koin, apakah akan muncul gambar atau angka? Meskipun bisa berpendapat bahwa peluang masing-masing hasil adalah sama. Tetapi tidak dapat dengan pasti mengatakan hasil yang akan muncul.

Dalam konteks ini, probability menyediakan kerangka kerja untuk mengkuantifikasi ketidakpastian tersebut. Dengan kata lain, adanya teori peluang ini bisa memberikan nilai numerik antara 0 dan 1 yang menggambarkan seberapa besar kemungkinan suatu peristiwa terjadi.

Kesimpulan

Dengan memahami dan menerapkan konsep probabilitas, Sahabat dapat membuat keputusan yang lebih tepat dan berinformasi dalam situasi yang tidak pasti. Analisis ini sangat penting dalam berbagai bidang, mulai dari ilmu pengetahuan, teknik, keuangan, hingga penelitian lainnya.

Tanpa memahami teori peluang ini, Sahabat akan sulit untuk menentukan seberapa valid dan andal suatu temuan penelitian atau sebuah keputusan di masa depan. Tentunya, diperlukan analisis matang untuk bisa benar-benar memutuskannya.