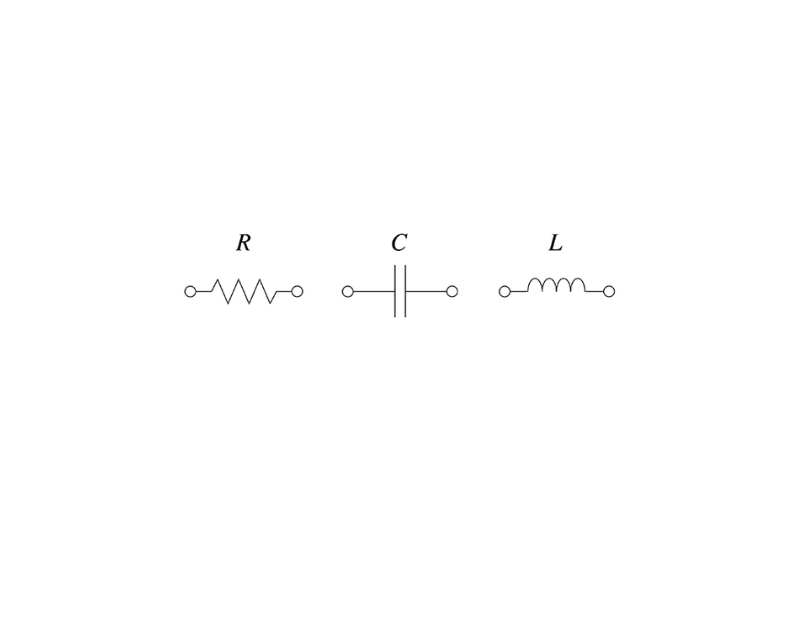Dalam dunia elektronik, terdapat istilah penting yang perlu dipahami, yaitu ” impedansi “. Istilah tersebut sebenarnya adalah tingkat hambatan terhadap arus listrik dalam suatu rangkaian. Pemahaman mendalam perlu dikuasai mengingat istilah ini penting untuk dipahami.
Meskipun terdengar sederhana, impedansi sebenarnya melibatkan tiga komponen utama, yaitu resistansi, reaktansi kapasitif, dan reaktansi induktif. Konsep ini sangat relevan dalam analisis rangkaian arus bolak-balik (AC) serta memiliki peran krusial dalam menjaga kualitas transmisi sinyal.
Pengertian Impedansi
Secara sederhana, impedansi adalah seperti “gangguan” yang dialami oleh arus listrik saat melewati suatu rangkaian atau perangkat. Bisa dianalogikan dengan hambatan dalam aliran air di sungai. Ketika air mengalir melalui sungai yang sempit atau berliku-liku, alirannya menjadi lebih lambat dan sulit.
Begitu pula dengan arus listrik, saat melewati rangkaian yang memiliki komponen seperti resistor, kapasitor, atau induktor, maka akan terjadi hambatan yang disebut impedansi. Ukuran satuannya adalah ohm, dan semakin tinggi hambatan, semakin sulit arus listrik untuk mengalir.
Istilah tersebut adalah salah satu konsep penting dalam dunia elektronika dan ilmu listrik. Hambatan ini adalah faktor yang mempengaruhi seberapa lancar arus listrik melalui rangkaian atau perangkat, seperti kabel dan transistor dapat mengalir.
Pertanyaan umum apa itu impedansi telah diuraikan secara lengkap melalui penjelasan di atas. Sahabat bisa langsung memahaminya dengan baik dari ulasan tersebut. Usai memahami pengertiannya, kini Sahabat bisa memahami jenis-jenis berikut:
Jenis Impedansi
Berdasarkan jenisnya, hambatan dapat diklasifikasikan menjadi beberapa variasi yang memiliki karakteristik unik. Berikut ini penjelasan yang lebih mendalam mengenai masing-masing jenisnya yang dapat Sahabat ketahui.
1. Akustik

Hambatan akustik merujuk pada besaran resistansi yang timbul dari propagasi gelombang suara dalam suatu medium. Nilai hambatan akustik dipengaruhi oleh berbagai faktor, seperti kedalaman medium, tekanan, suhu, dan faktor-faktor lainnya yang mempengaruhi perambatan suara dalam medium tersebut.
2. Kapasitif

Hambatan kapasitif terjadi ketika reaktansi kapasitif mendominasi dibandingkan reaktansi induktif dalam suatu rangkaian. Ini terjadi khususnya ketika bagian imajiner dari kapasitor mengalami perubahan arus, menghasilkan perubahan dalam hambatan.
3. Induktif
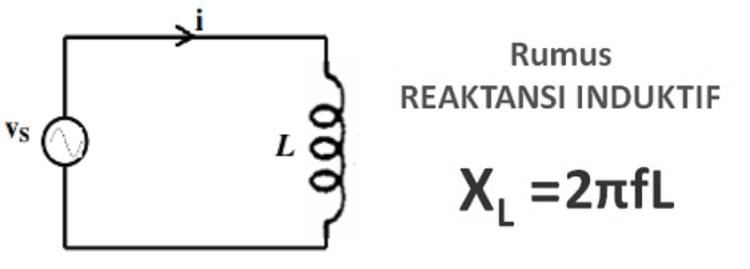
Berikutnya adalah hambatan induktif terjadi saat reaktansi induktif dalam suatu rangkaian memiliki nilai lebih besar daripada reaktansi kapasitifnya. Kondisi ini dapat terjadi pada komponen seperti kumparan, di mana hambatan terhadap perubahan arus lebih besar dibandingkan aspek imajiner dalam rangkaian.
4. Resistif
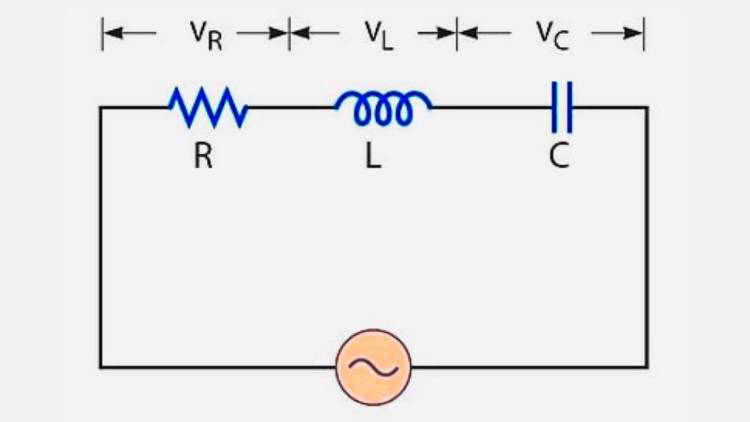
Lalu yang satu ini muncul ketika nilai reaktansi dalam rangkaian arus searah berada pada titik nol. Ini berarti bahwa hambatan terhadap arus searah pada suatu komponen atau rangkaian adalah hampir eksklusif terhadap aspek resistifnya, tanpa reaktansi kapasitif atau induktif yang signifikan.
5. Ekivalen
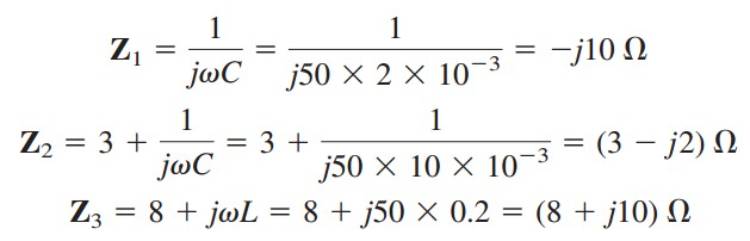
Hambatan terakhir berjenis ekivalen merujuk pada kondisi di mana total nilai hambatan dalam suatu rangkaian adalah sama. Konsep ini sering diterapkan dalam analisis jaringan, terutama dalam situasi di mana beberapa rangkaian digantikan dengan satu rangkaian yang setara.
Contohnya adalah penggunaan rangkaian ekivalen pada resistor, baik dalam rangkaian seri maupun paralel, untuk mempermudah analisis rangkaian. Dengan memahami berbagai jenisnya, Sahabat dapat lebih mendalam dalam merancang dan menganalisis rangkaian elektronik yang melibatkan arus listrik.
Kriteria Impedansi
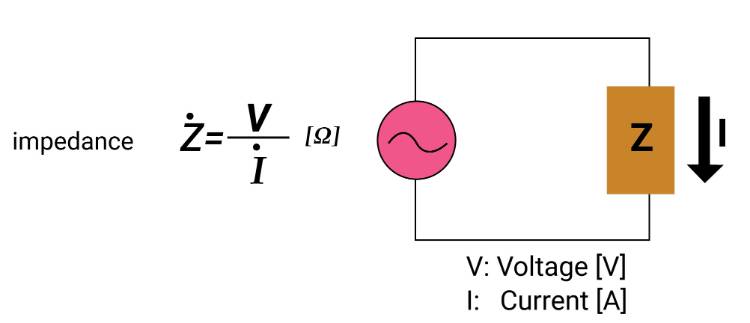
Impedansi, atau dalam istilah umum juga disebut sebagai hambatan dalam rangkaian listrik, memiliki sifat yang menarik untuk dijelajahi. Dalam jenis rangkaian ini, nilai memiliki hubungan yang berbanding terbalik dengan besarnya hambatan.
Artinya, semakin besar nilai hambatan dalam suatu rangkaian, maka semakin tinggi pula nilai yang dibutuhkan. Sebaliknya, semakin kecil hambatan, maka terjadi kebalikannya. Berikut beberapa karakteristik umum tentang hambatan yang penting Sahabat ketahui:
1. Hambatan Bukan Hanya untuk Arus Bolak-Balik
Hambatan tidak hanya berlaku untuk arus bolak-balik, yang berubah arah secara berkala, tetapi juga berlaku untuk jenis arus searah. Namun, penting untuk dicatat bahwa dalam kasus arus searah, konsep memerlukan adanya konsep fasa hambatan agar dapat diterapkan secara tepat.
2. Hubungan Tegangan dan Arus
Tegangan pada suatu hambatan memiliki hubungan khusus dengan arusnya. Hubungan ini sering kali dijelaskan menggunakan hukum Kirchoff dan prinsip-prinsip lain dalam analisis rangkaian listrik.
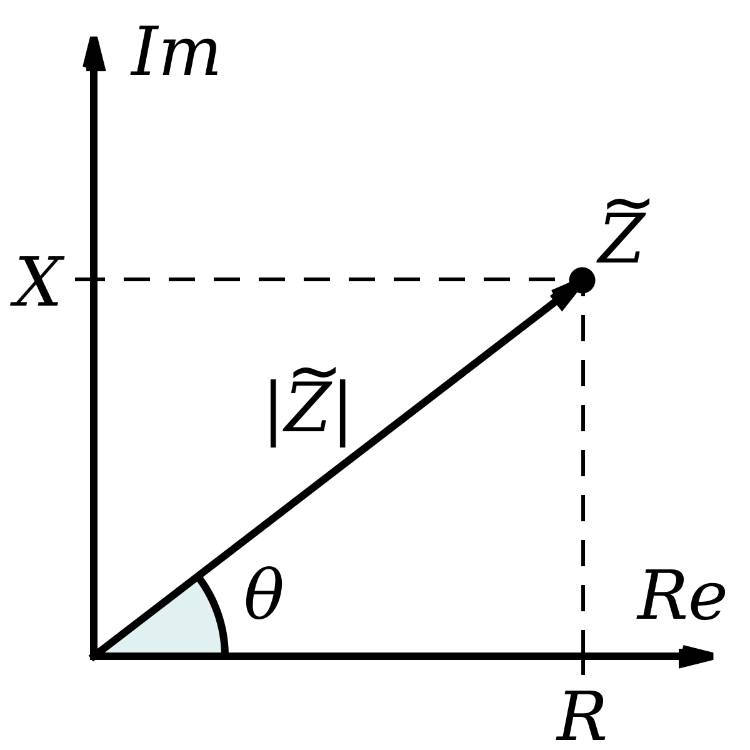
3. Representasi Nyata dan Imajiner
Dalam konteks hambatan, komponen nyata dan imajiner dari nilai hambatan seringkali dijelaskan dalam bentuk binomial. Hal ini memungkinkan Sahabat untuk memahami bagaimana hambatan dan komponen reaktif berinteraksi dalam perhitungan impedansi.
4. Simbol dan Notasi
Hambatan diwakili oleh simbol “Z” dan sering kali didefinisikan dalam kaitannya dengan admitansi, yang juga dinyatakan dengan simbol “A”. Konsep ini menggambarkan konversi antara hambatan dan reaktansi dalam rangkaian.
Dengan pemahaman tentang karakteristik ini, Sahabat dapat menggali lebih dalam tentang bagaimana hambatan memainkan peran kunci dalam mengatur aliran arus listrik dalam berbagai rangkaian dan perangkat elektronik.
Baca Juga: Kapasitor (Kondensator) : Pengertian, Cara Kerja, Jenis
Rumus Perhitungan Impedansi
Pastinya terdapat rumus yang perlu Sahabat ketahui agar bisa memperhitungkan hambatan dengan tepat. Berikut adalah rumus perhitungan untuk berbagai jenis komponen dalam rangkaian listrik:
1. Hambatan Resistif (Z = R)
Pada komponen resistif, seperti resistor, hambatan secara langsung berbanding lurus dengan nilai resistansinya. Oleh karena itu, hambatan di dalam rangkaian resistif hanya sama dengan nilai resistansinya.
2. Hambatan Kapasitif (Z = 1 / jωC)
Pada komponen kapasitif, hambatan dipengaruhi oleh frekuensi arus bolak-balik (ω) dan kapasitansi (C) komponen tersebut. Rumusnya adalah Z = 1 / (jωC), di mana “j” adalah bilangan imajiner (√(-1)).
3. Hambatan Induktif (Z = jωL)
Komponen induktif, seperti induktor, memiliki hambatan yang tergantung pada frekuensi arus bolak-balik (ω) dan nilai induktansinya (L). Rumusnya adalah Z = jωL.
4. Hambatan RLC (Z = √(R^2 + (Xl – Xc)^2))
Dalam rangkaian yang mengandung komponen resistif (R), induktif (L), dan kapasitif (C), hambatan total (Z) dapat dihitung menggunakan rumus di atas. Di sini, Xl adalah reaktansi induktif (jωL) dan Xc adalah reaktansi kapasitif (1 / jωC).
Cara menghitung ini bisa Sahabat kuasai dengan berlatih contoh soal. Dengan banyak berlatih, maka akan semakin menguasai rumus dan bisa menghitung dengan cepat.
5. Hambatan Total dalam Rangkaian Campuran
Dalam rangkaian yang lebih kompleks dengan kombinasi komponen resistif, kapasitif, dan induktif, hambatan total dihitung dengan menggabungkan efek masing-masing komponen menggunakan hukum Kirchoff, prinsip impedansi, dan prinsip-prinsip analisis rangkaian.
Rumus hambatan kasar di atas bisa Sahabat pahami dan coba untuk dihitung terlebih dahulu. Apabila sudah memahaminya dengan baik, maka cara untuk menghitungnya pun akan mudah untuk dikuasai.
Resistansi yang berada pada rangkaian yang sama lalu dijumlahkan maka akan menjadi total impedansi. Rumus di atas beserta penjelasan lengkapnya bisa Sahabat simak dengan mudah dan langsung dapat dipraktekkan.
Kesimpulan
Sahabat perlu diingat kembali bahwa impedansi adalah hambatan khusus yang dihadapi arus listrik saat melewati rangkaian atau komponen tertentu. Ini dapat diibaratkan dengan hambatan dalam aliran air di sungai.
Selain pengertian, Sahabat bisa memahami jenis-jenis, hingga pada kriteria beserta cara perhitungan. Usai memahaminya dengan baik, maka kedepannya saat melakukan analisis rangkaian listrik bisa lebih baik daripada sebelum mengetahui akan seluk beluk hambatan kasar tersebut.
Baca Juga: Rumus Segitiga Daya Listrik dan Contoh Penggunaannya